Twitter Analysis
While I have a Twitter account (@sereue), I rarely ever tweet. I use it primarily to follow celebrities, favorite organizations, and local news. Knowing this, I wasn’t certain how interesting my Twitter network would be, or how connected my ‘friends’ were.
Using the Wakita-Tsurumi method, 12 groups were found in my Twitter network, each created around an interest of mine (See Figures 4 – 15 below). Looking at the constituents of each group, it is easy to see that I like to follow funny people. So many of the groups have comedians, comedy writers, and/or actors from comedic shows. Some groups even revolve around a TV show, such as Glee, Mythbusters, How I Met Your Mother, and psych. Others show my interest in Science and Mathematics. Nearly all of the groups are connected to each other (see Figure 2). The only isolate group is Group 9, the “Math Facts” group. This means that for each group, except Group 9, there is at least one person acting as a boundary spanner to at least one other group.
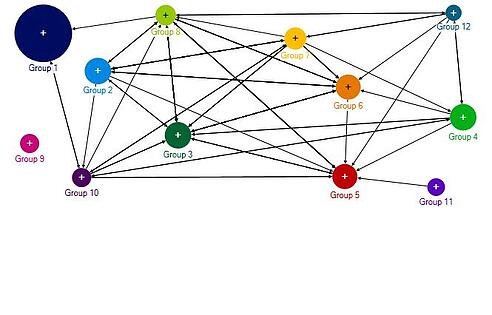
Figure 2: Group-to-group Interaction
Group 9 is interesting for another reason. Its graph contains 5 nodes and is complete, that is, each node is connected to every other node in the group (see Figure 12 below). Given that each account tweets facts about a given aspect of mathematics and are all similarly named (@AlgebraFact, @StatFact, etc.), it is possible they share a common owner. In a professional setting, it would be beneficial to be able to recognize similar structures, because information held by one account would very quickly spread to the other accounts.
In the overall graph, @SteveMartinToGo, @edhelms, @ActuallyNPH, @ZooeyDeschanel, @alydenisof, @simonpegg, and @donttrythis are the major information brokers, with the highest betweenness centrality scores [31.752, 69.900]. This means that for information traveling along the shortest path between two accounts, it will likely pass through one of these people. If these accounts were removed, they would leave large, gaping holes in the network, which would slow the flow of information, if not halt it completely.
The top Centers of Attention in the overall graph are many of the same people who are Information Brokers: @SteveMartinToGo, @edhelms, @ActuallyNPH, @alan_tudyk, @alydenisof, @donttrythis, @simonpegg, @ConanOBrien, and @ZooeyDeschanel. With eigenvector centrality scores in the range of [0.015, 0.020], these accounts are following or followed by other accounts with many followers/friends. This puts them in the position of being Influencers within the Network. It is also interesting to note that within their respective groups, these accounts act as hubs, connecting many other group members to each other.
That the accounts having the greatest Influence, and are on the majority of ‘shortest paths’ are celebrities comes as no surprise (see Figure 16). Celebrities are, by definition, very popular people, so many people would want to connect with them. Working within the entertainment industry also puts many different celebrities together at different times for different shows/events, so it is also not surprising that celebrities follow each other, especially when they have worked on a project together.
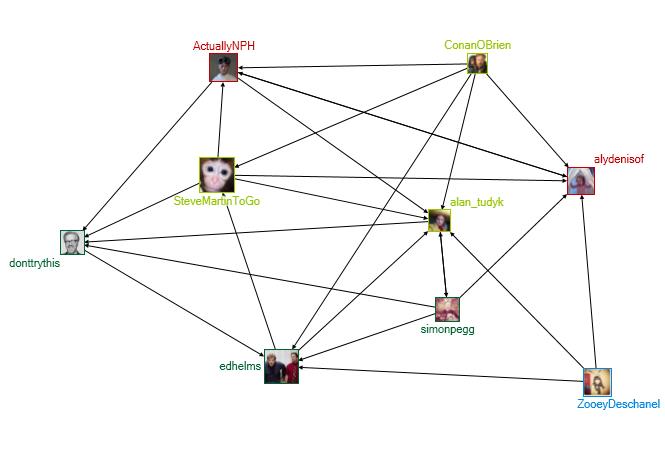
Figure 16: Information Brokers and Centers of Attention
If this was a professional network and I wished to disseminate information, I would target the group of Information Brokers and Centers of Attention first. A message tweeted by one of these people would spread quickly through the network, given that it was a message that people wanted to retweet. But the work wouldn’t stop there, as some members of the network are not connected to everyone else, such as the Math Facts group. It would be important to either find a way to connect that group to the others, or to make an effort to specifically target this group for every message that went out. Careful attention would also need to be paid to the directionality of the relationships. If a message is started at an account that follows many people, but does not have many followers of its own, it is less likely to make it through the network quickly than a message originating from an account with many followers and few friends.
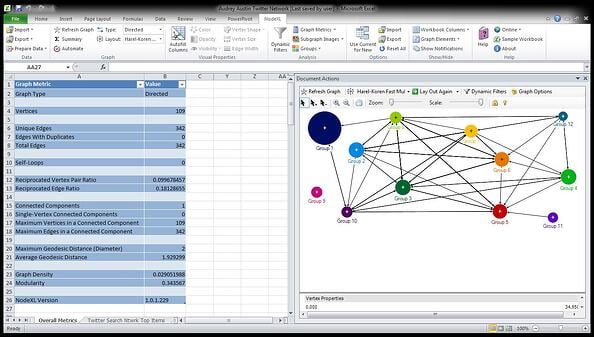
Note: Since directionality is important in the Twitterverse (who follows whom), I decided to use a directed graph. However, the default setting is to have the arrow point from the follower to the friend. This is counter-intuitive as far as the flow of information is concerned. In order to follow information as it moves through the network, I switched the Vertex 1 and Vertex 2 columns on the Edge tab.
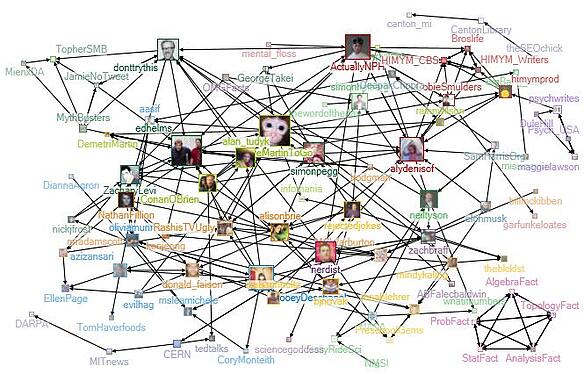
Vertex size mapped to eigenvector centrality, vertex opacity mapped to betweenness centrality.
----------
If you would like to contact me, please see my LinkedIn profile.
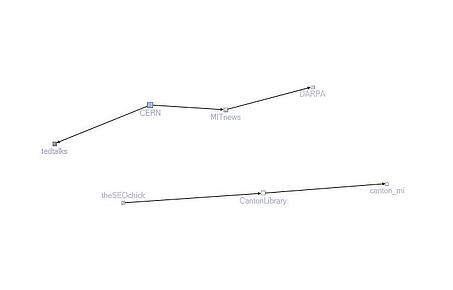
Figure 4: Group 1: Local Interests and Science
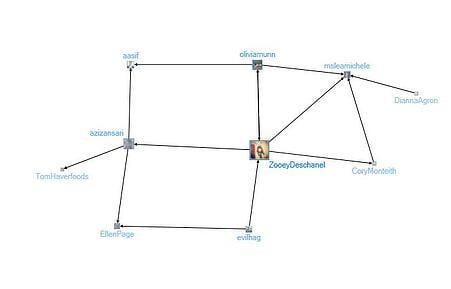
Figure 5: Group 2: Young Comedic People
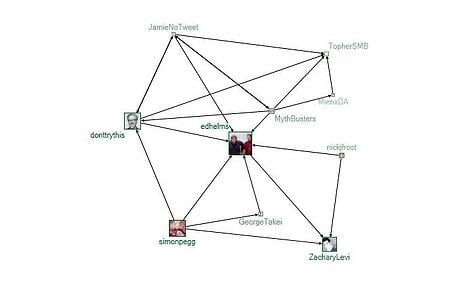
Figure 6: Group 3: Mythbusters
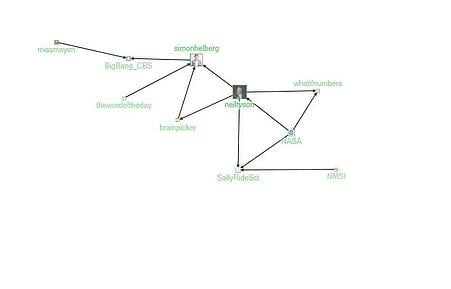
Figure 7: Group 4: More Science
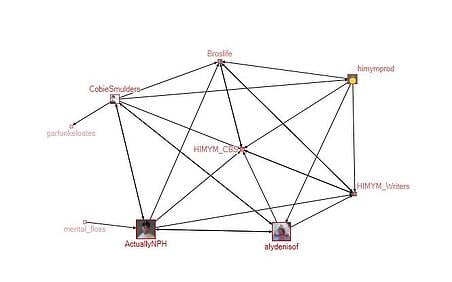
Figure 8: Group 5: How I Met Your Mother
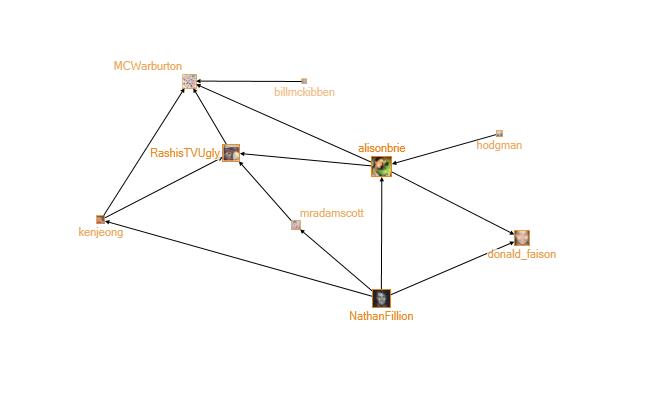
Figure 9: Group 6: More Comedians
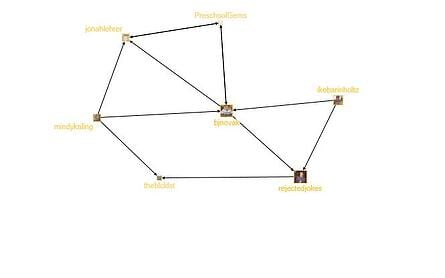
Figure 10: Group 7: Comedy Writers
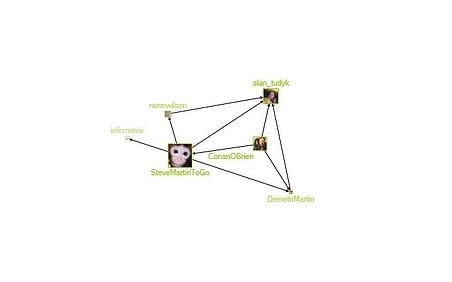
Figure 11: Group 8: Older-ish Comedians
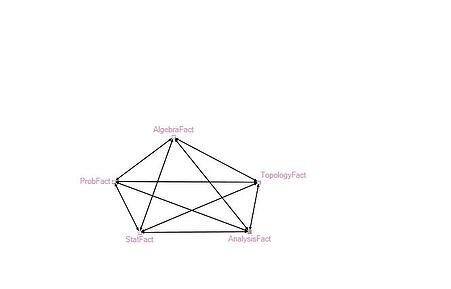
Figure 12: Group 9: Mathematics
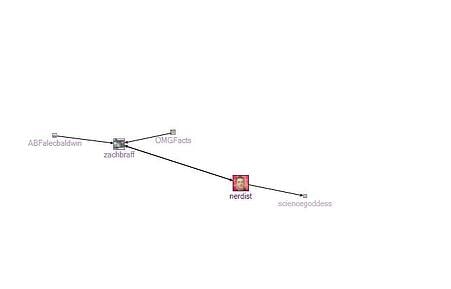
Figure 13: Group 10: Geeky Comedy
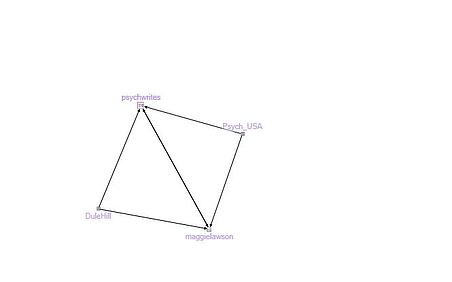
Figure 14: Group 11:




